数学中sgn是什么意思（特殊函数大家族——你知道哪几个？）

这里所说的特殊函数，不是初等函数，更不是复合函数，我们来了解一下，都有哪些比较特殊。

下面我们就来一一列举这几个特殊的函数。

函数一：符号函数是数学上的Sgn 函数返回一个整型变量，指出参数的正负号，符号函数有且只有一个。

如下所示：

函数二：取整函数

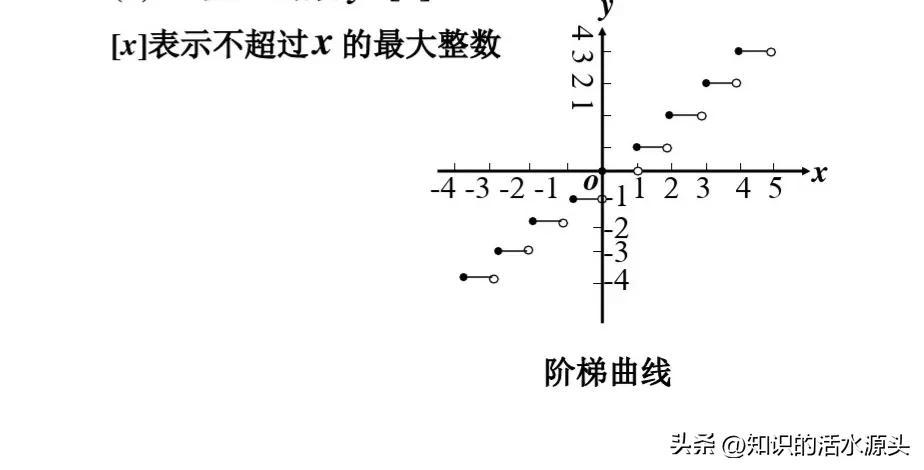
概念：函数y=[x]被称为取整函数，也可以称为高斯函数。其中不超过实数x的最大整数称为x的整数部分，记作[x]。

因为这个函数的特殊性，该函数被广泛应用于数论，函数绘图和计算机等多个领域。

从图像我们可以看出来，他是由左向右成阶梯式的。

举例：[x]表示不超过x的最大整数，就是说[2.4]＝2，[-0.7]＝-1，还有很多，大家可以类比记忆。

函数三：狄利克雷函数。

这个函数大家应该不是很陌生，在狄利克雷函数中，大家会发现，他的函数值永远只有两个。

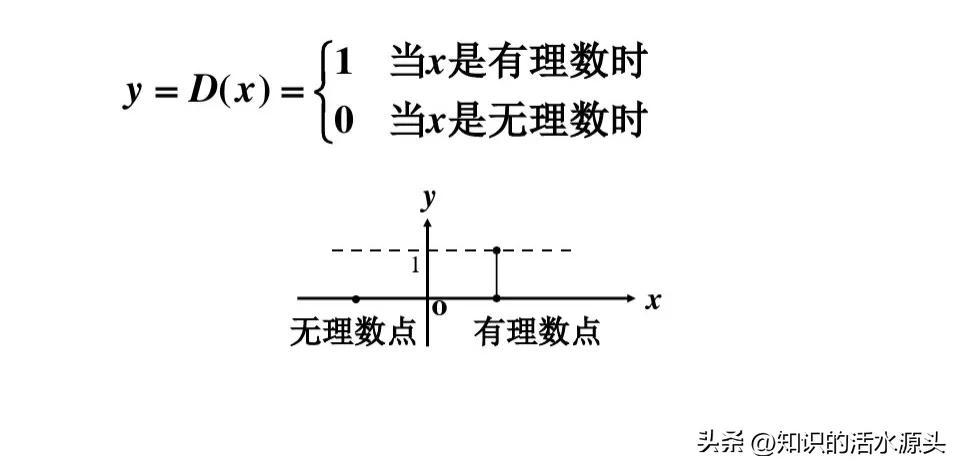
概念：他是定义在实数范围上、值域不连续的函数。

狄利克雷函数的图像是以Y轴为对称轴，是一个偶函数，并且每处都不连续，每一处极限都是不存在的，并且不能黎曼积分。

公式定义：

实数域上的狄利克雷函数表示为如下形式，其中k，j为整数。

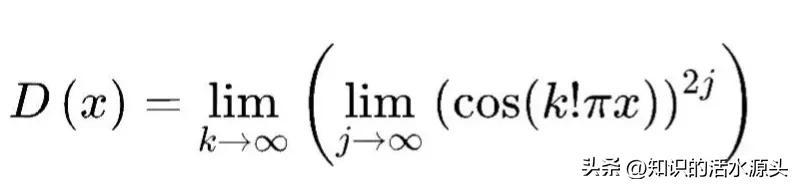
如下所示：

函数四：取最值函数。

这个比较好理解，在我们的函数中，都存在着最值问题，有些函数有最值，而有的函数是不存在最值得。

最值分为最大值和最小值，在某个区间内，如果存在最高点，并且有意义，那么就称为最大值，反之就是最小值。

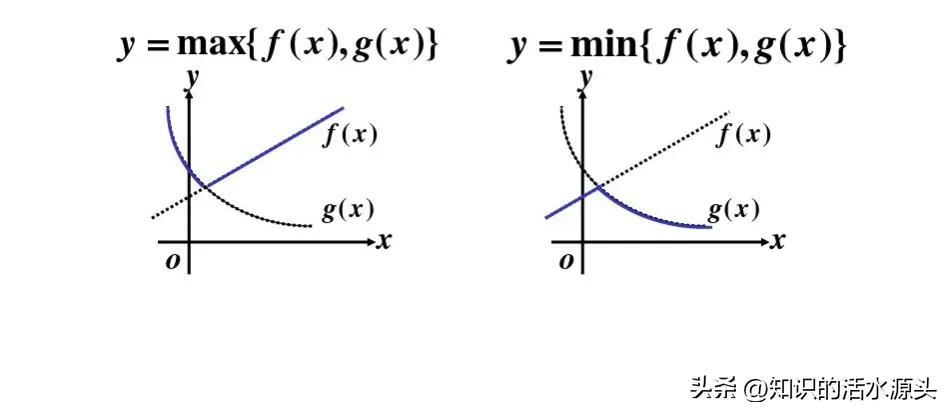
函数五：分段函数。

在自变量的不同变换范围中，对应法则用不同的式子来表示的函数，称为分段函数。

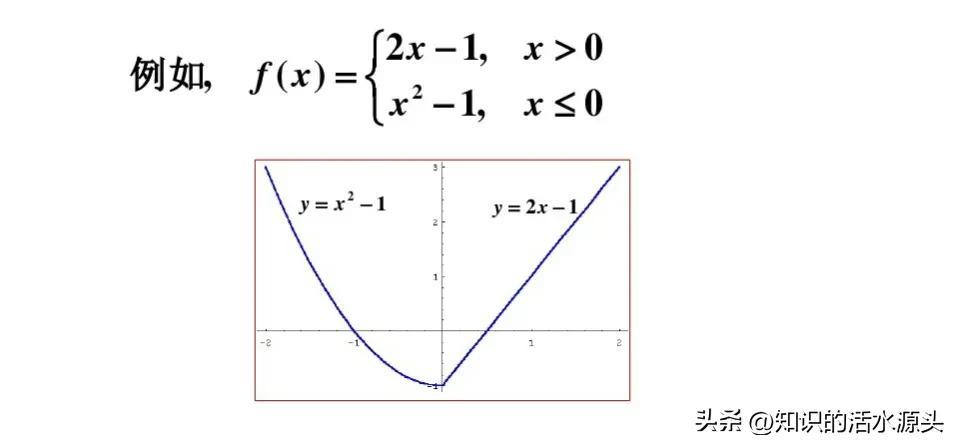
分段函数模型比较多，大家可以自行参考。